
以前の記事でご紹介した北海道の温度データのグラフを一つの式でまとめられそうな予感がしたのですが、気づけばもう夏。
がしかし、先日やっと見つけました。極寒で冷えていく車内の温度変化を表すであろう数式を。
目次
ハイエース冷却のモデル
※熱伝導については、こちらのサイトを参照しました。 もっと知りたい! 熱流体解析の基礎
極寒で冷えていくハイエースを、下図のようにモデル化しました。
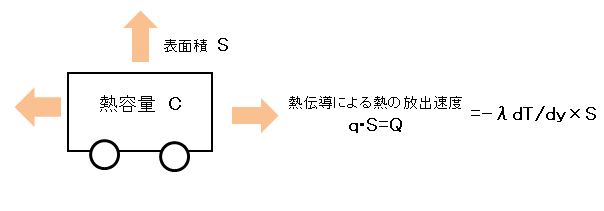
(ちょっとひどい図ですが、それは置いておいて)
ハイエースの熱容量をC (J/℃)
ハイエースの全表面積を S (m2)
熱伝導によるハイエースから外界への熱流速を q (W/m2)とします。
このとき、ハイエース車体の熱伝導率をλ(ラムダ)とすると、熱の放出速度Q=qS= -λ×dT/dy×S
ここで、dT/dyは温度勾配と呼ばれ、温度の高い部分と温度の低い部分の間の温度の勾配のことを指しています。
下記を仮定して話を単純化します。
1.ハイエースからの熱の放出は、熱伝導によってのみなされる。(対流、輻射による熱の移動は無視する)
2.ハイエースから外界への熱伝導は、すべて同じ温度勾配でなされる。
3.この温度勾配の値は、ハイエース車内と外界の温度差に比例する。
すると、
4.ハイエースの温度の低下速度は熱の放出速度に比例し、
5.熱の放出速度は温度勾配に比例するので、
ハイエース内部の温度の低下速度はハイエース車内と外界の温度差に比例する
ということになります。
つまり、式で書くと
dT/dt(温度の低下速度)=-Λ×車内外の温度差 … (a)
ここで、tは時間を示し、Λ(大文字のラムダ)=λ×S です。
ハイエース車内と車外の温度差と、冷却の関係式は?
もはや微積分の記憶も怪しく、自力でひねり出すのは不可能。そのうち見つかるだろうと思っていたら、やっとみつかりました。
比例定数として使われている記号、λ(ラムダ)まで同じなのは偶然でしょうか。
そして、上記ウィキペディアの記事に沿って(a)の式を解くと、
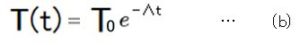
となります。
T(t)は、時刻tにおけるT (この場合、車内の温度) の値、T0は、時刻0におけるTの値、eは自然対数の底(=2.71828…)です。
つまり、話を単純化するために用いた前述の1~3の仮定のもとでは、ハイエース車内の温度変化と時間の関係は(b)の式によって求められるはずです。
問題は、この式が現実に合っているかどうか です。
北海道旅行での測定データとの比較
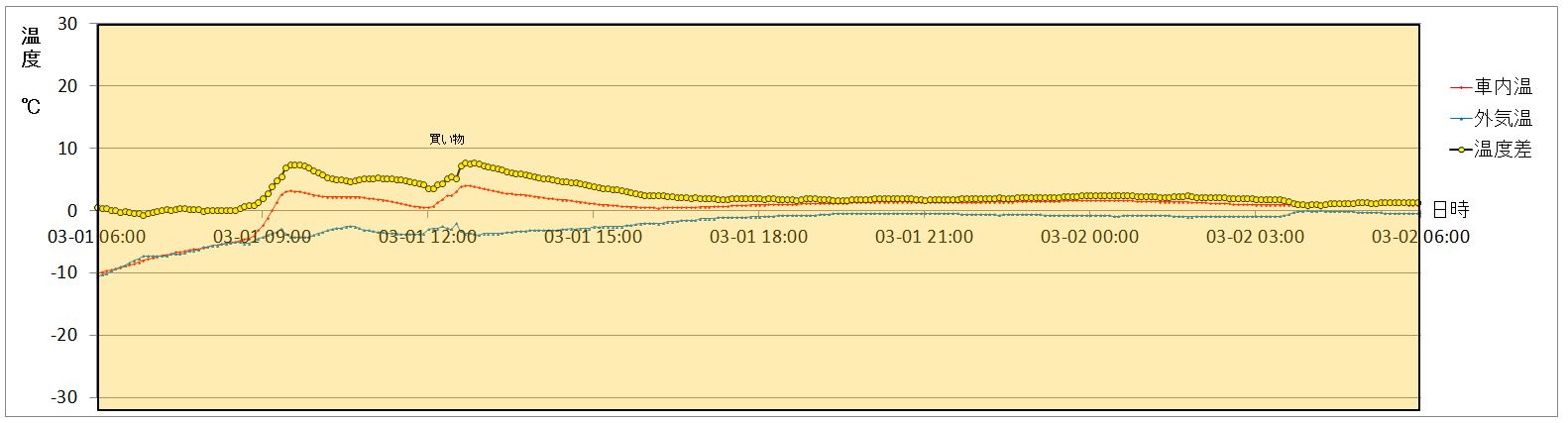
元になる温度のグラフ
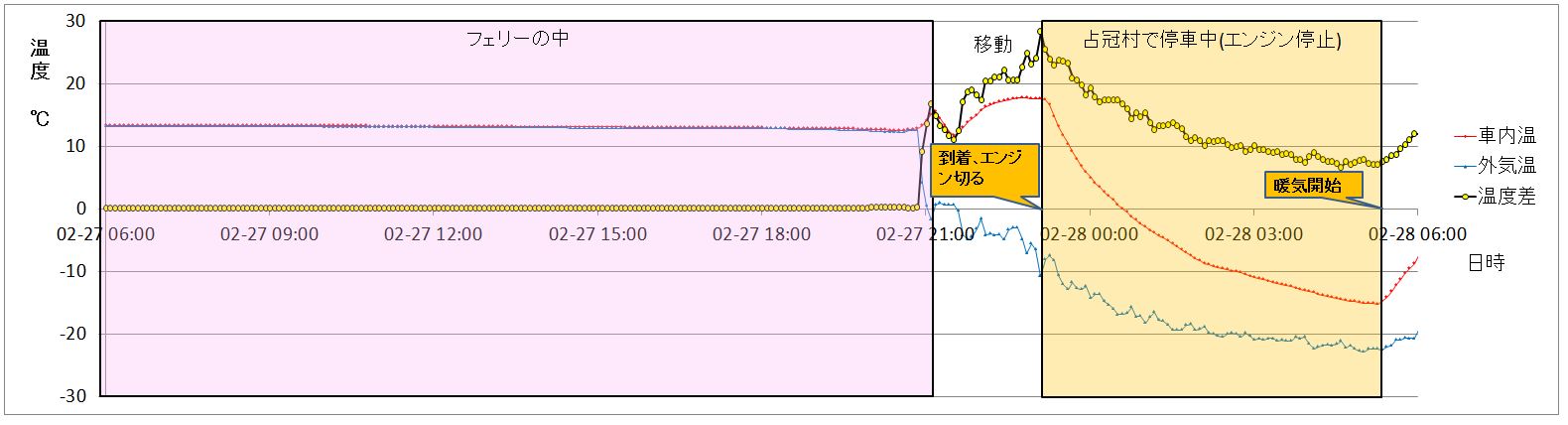
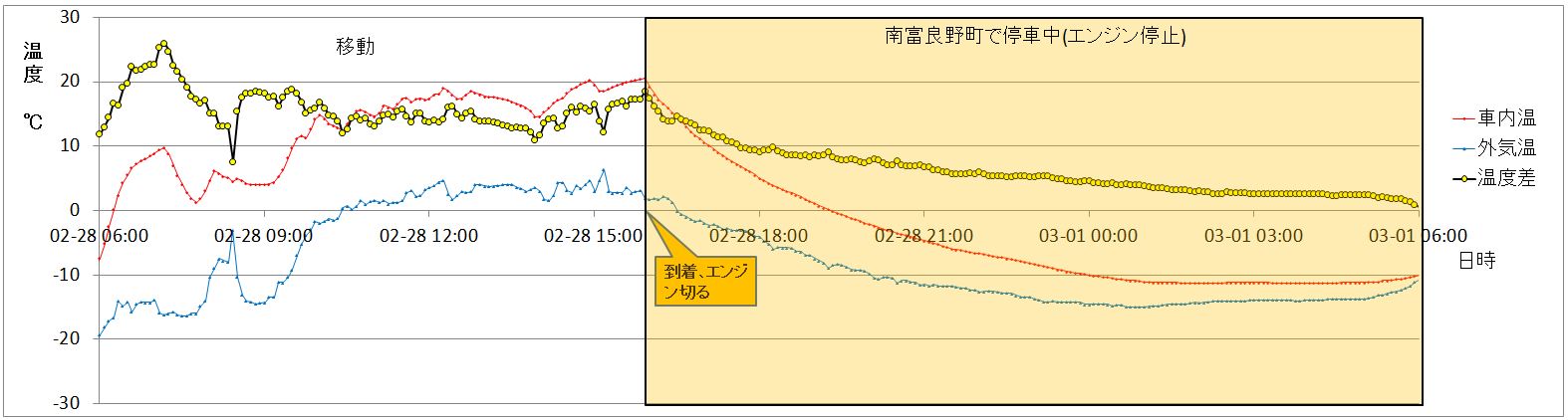
北海道では、車内(ベッドキットの上)と車外の気温を温湿度データロガーで10分おきに出発から帰着まで測定を行いました。
このときのデータをグラフ化したのが以下の3つのグラフです。
赤い線が車内温度、青い線が外気温度、そして黄色い線が車内温度と外気温度の差(以下、温度差と記載します)です。
下記の3つは、順番に温度差が高いもの、中くらいのもの、低いものを選んでいます。(たまたま、3日間の連続したデータになっています)
なお、グラフ中のピンクの網掛けはフェリーで航行中、オレンジの網掛けは基本的にエンジンが止まって停車していることを示します。なお、3つめのグラフは道の駅南ふらので大雪のため動けなくなった日で、道の駅でエンジンを切って停車していましたが、時折買い出しや除雪車の作業の邪魔にならないよう車を移動させるためにエンジンを掛けており、そういった際に若干車内温度が上下しています。
温度グラフに重ねてみるための指数関数的減衰のグラフ
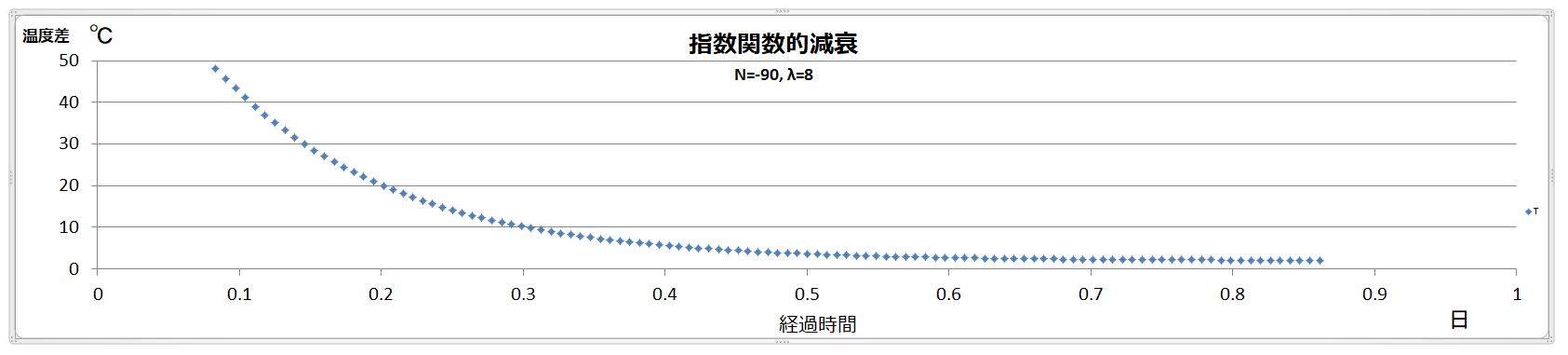
これらについて、エンジンを切って温度が低下しているときのグラフが上記(b)のグラフとうまく重なるよう、T0とΛの値を調節し、T0=90 (℃)、Λ=8 としました。このときのグラフは下記の通り。
横軸は時間で、単位は「日」です。右端の1まで行くと一日=24時間経過、ということです。
縦軸は、前掲の温度差のグラフと重ねるので、単位は℃としています。

重ねてみると…
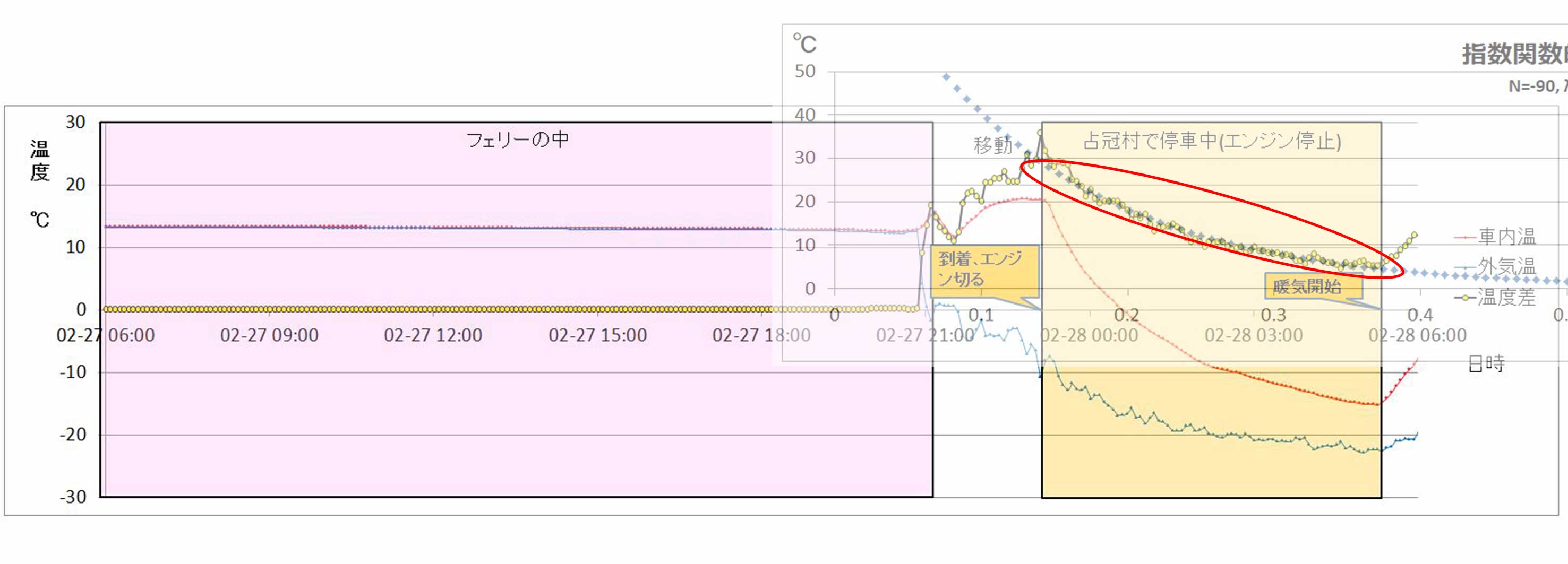
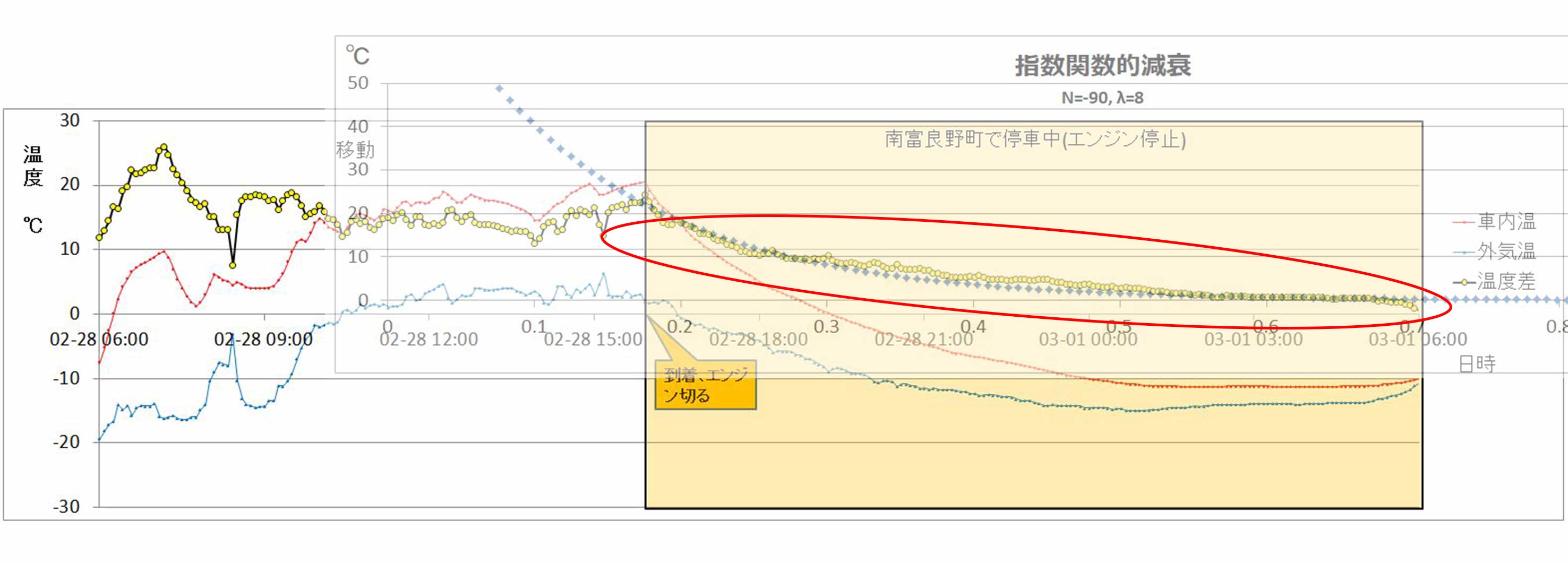
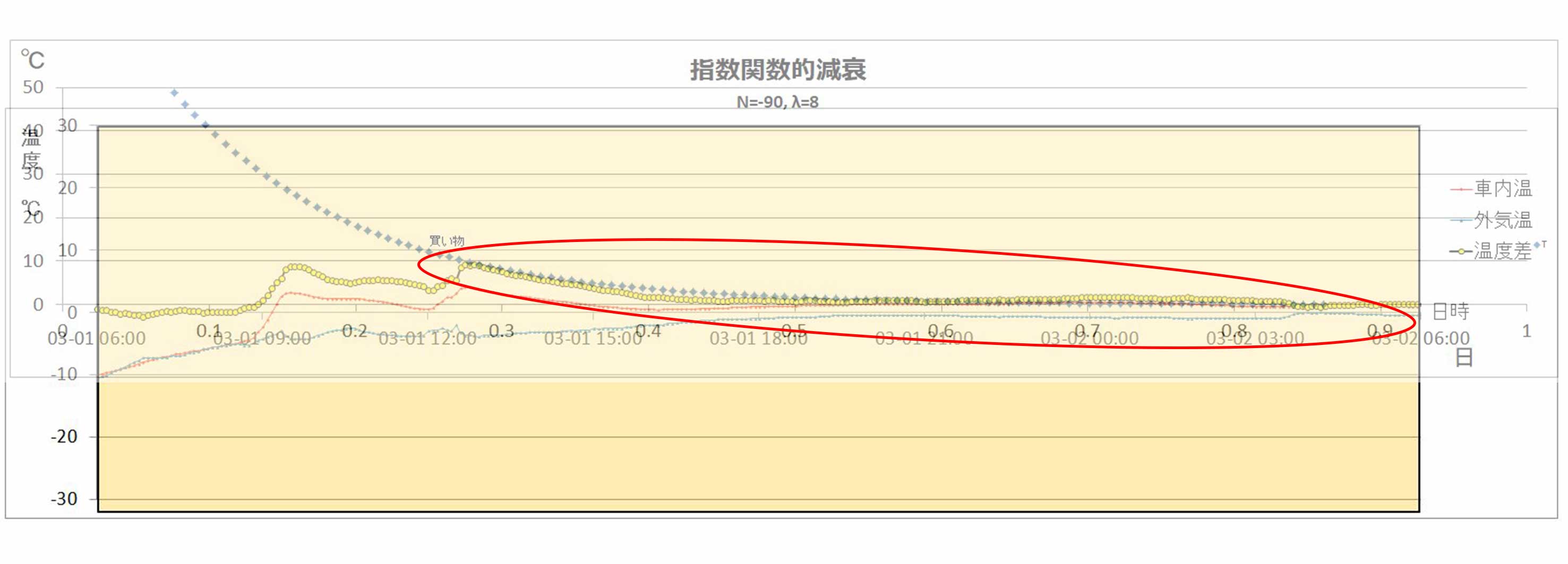
ちょっとごちゃごちゃしていますが、3枚それぞれの温度グラフにおいてハイエースが停車して温度が下がって行っている部分に指数関数的減衰のグラフを重ねてみました。
赤い楕円で囲んだ部分が両者のグラフを重ねた部分で、指数関数的減衰のグラフはフォトショップで半透明にして重ねました。
どうでしょうか。かなり綺麗に一致していると思いませんか?
2月27日のグラフ
温度差が30℃近くあるところから温度差5℃くらいまで低下している部分でグラフがほぼ一致しています。
2月28日のグラフ
次は、温度差がもう少し低めの20℃くらいから3℃くらいまで低下している部分。ここもほぼ一致しています。
3月1日のグラフ
最後は、温度差10℃くらいからもう下がらないところで平衡状態のまま一定を保っています。
この区間もほぼ一致。
結果
以上三枚の温度グラフは、いずれもT0=90、Λ=8とした場合の指数関数的減衰のグラフの一部を切り取ったものにほぼ一致することが分かります。
結果の利用
3月1日の温度グラフと指数関数的減衰のグラフを重ねたものは、エンジンによる強力な加熱無しで12時間以上放置しているのですが、最終的には温度差は2℃程度まで下がっています。従って、冷却時間と温度差の関係は、概ね下記のようになると思われます。平衡状態で+2℃だったことを考慮し、グラフを上方向に+2だけ持ち上げています。
さて、これを使うと何ができるでしょう?
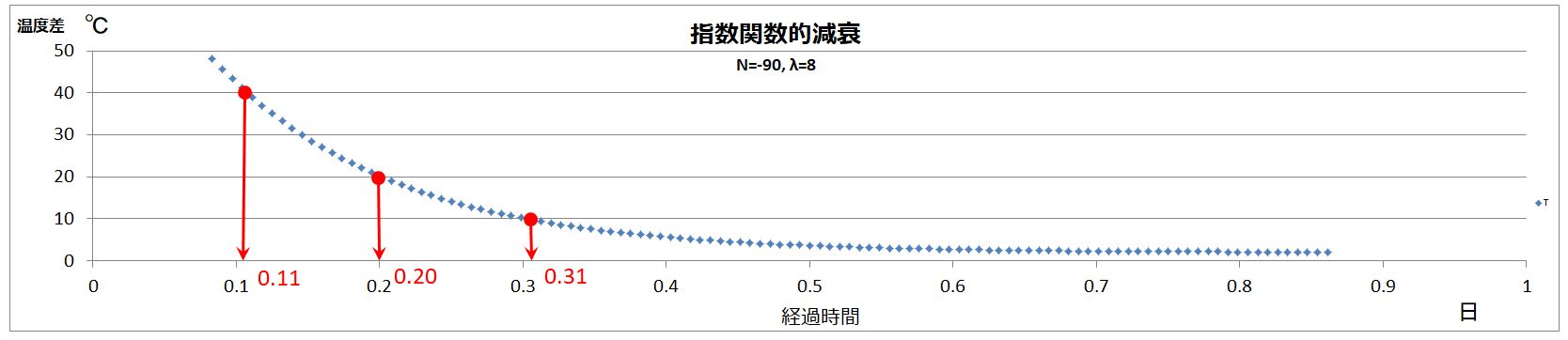
例えば、下記の通り、
温度差40℃から10℃に下がるまでの時間は、0.31-0.11=0.20日=4.8時間
温度差20℃から10℃に下がるまでの時間は、0.31-0.20=0.11日=2.64時間 であることが分かります。
従って、最初に温度差を40℃まで上げておくと、20℃までしか上げない場合に比べて温度の低下を約二時間遅らせることができる、ということが分かります。
温度差40℃というと暑そうですが、外気温がマイナス20℃なら、+20℃ですから、きつめに車内を暖房すれば達成できそうです。
(そして、温度差が+10℃だとしても、外気温が-20℃なら、車内は-10℃なわけで、十分寒いですが)
そしてまた、翌朝の最低気温が分かっていれば、そのときの気温がどれくらいになるのかが予想できるので、それが低すぎるのであれば夜中に起きてアンドリングして車内温度を上げてこれをアップさせることも可能です。
以上、読んでくださりありがとうございます。
【寒さ対策】関連記事の一覧はこちらです。
