
Overview: Generate a equation which explains the relationship between the temperature of THERMOS bottle FFX-900 content, outside temperature, and elapsed time.
前回の記事に続き、今回は、サーモス山専用ボトルFFX-900に入れた熱湯が何時間後に何度に冷えているかを算出する公式を作ってみます。
以前の記事で、極寒に置かれたハイエースの温度がどのように変化するかを算出できる公式をご紹介したことがありました。
まず以前の記事と同様、指数関数的減衰の式で山専用ボトルの中身の冷却状況が計算できるような定数の値を求め、次にこれを測定値のグラフにプロットしてその有効性を検証します。
目次
水筒の冷却を近似できる式は?
指数関数的減衰
指数関数的減衰は、下記の微分方程式で表されます。

これはつまり、
ある量(この場合はN)が減少するスピードは、Nの大きさに比例する … ①
ということを表しています。
Q値
住宅の断熱度合いを表す数値として、熱損失係数(Q値)を用いますが、この値は、熱が逃げる速度を表しています。この値が小さいほど、熱が逃げにくく、冬は暖かいことを表しています。
そして、Q値の単位は、W/m2・K (W=ワット、K=絶対温度)
つまり、Q値は単位面積、温度差1度あたりで熱が逃げる速度を表している定数ですから、逆に考えると
- 熱が逃げる速度は外気との温度差に比例する
ということです。
そして、もう一つ、一般的な事実として、
- ものの温度は、逃げた熱量に比例して低下する
この二つを合わせると、
ものの温度は、外気との温度差に比例した速度で下がる … ②
ということになります。
これはつまり、熱いものはどんどん冷えますが、ある程度冷えてくると冷えるスピードもゆっくりになるということで、日常の経験に一致しています。
以上より
②のものの外気との温度差は、①のNと同じ性質をもつので、指数関数的減衰の微分方程式を水筒の冷却状態を近似するのに使える(かもしれない)ことがわかります。
今回のグラフの近似式は?
ある時刻tにおける、ものの温度と外界の温度の差 T(t)は、T0(時刻ゼロの時のT(t)の値)と、定数Λ(ラムダ)を用いて、下記のように表すことができます。(T0、T(t)は、外界との温度差であって、温度ではないことに注意)
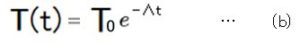
なお、Λは、条件ごとに違ってきますので都度計算する必要があります。(条件とは、水筒の種類や中に入れる水の量など)
(1) 熱湯を入れて室温(25℃)に放置した場合の温度変化
熱湯を山専用ボトルに入れた直後の温度が98.5℃なので、
時刻ゼロにおける外界(この場合は室温)との温度差 T0=98.5-25=73.5℃、
測定開始から12時間43分後(=12.7時間後)に、温度が80.5℃なので、このときの外界との温度差は 80.5-25=55.5℃
Λ=(LN(55.5/73.5))/(-12.7)=0.022118 (LNは、自然対数)
よって、この場合の近似式は、時刻tにおける温度差をT(t)とすると、
T(t)=73.5*e (-0.022118)*t
このときの山専用ボトルの中身の温度は、
T(t)+25= 73.5*e (-0.022118)*t+25
この式の値をグラフ上にプロットすると、下図のようになります。
大きなオレンジ色のマーカーが今回の測定値、小さな黒いマーカーがこの近似式のプロットです。非常にきれいに近似できていますね。
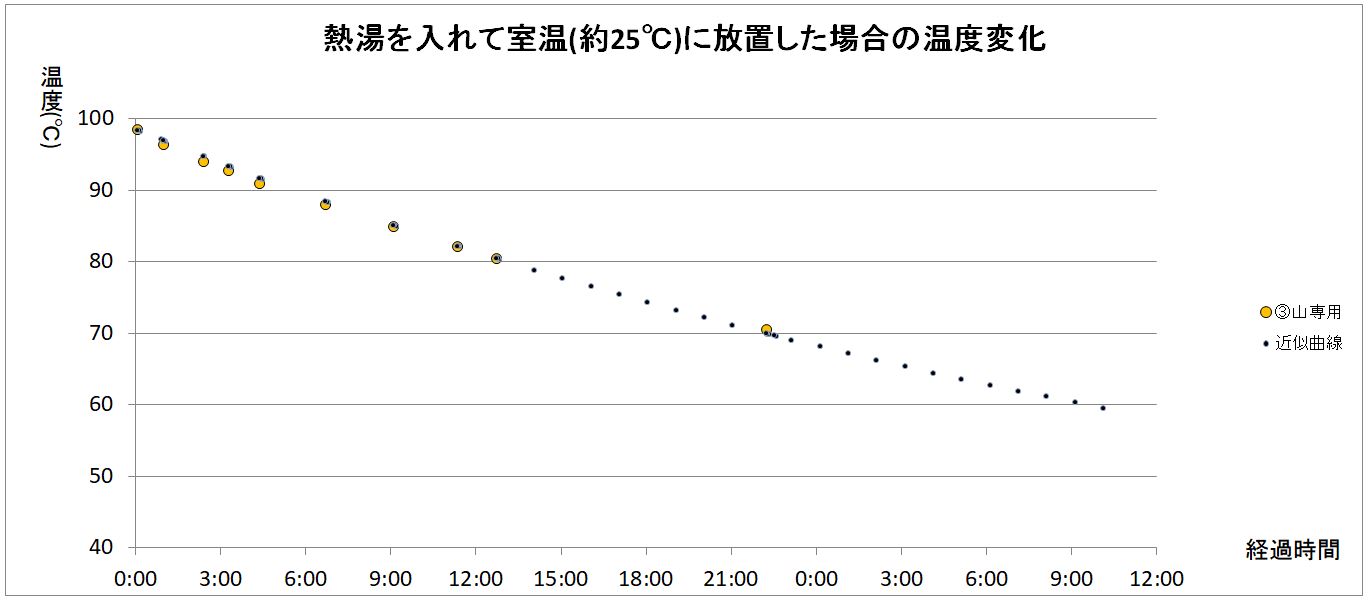
(2) 熱湯を満量入れて冷凍室(マイナス20℃)に格納した場合の温度変化
熱湯を山専用ボトルに入れた直後の温度が98.7℃なので、
時刻ゼロにおける外界(この場合は冷凍室)との温度差T0=98.7+20=118.7℃、
測定開始から13時間53分後(=13.9時間後)に、温度が70.4℃なので、このときの外界との温度差は 70.4+20=90.4℃
Λ=(LN(90.4/118.7))/(-13.9)=0.019594
よって、この場合の近似式は、
T(t)=118.7*e (-0.019594)*t
このときの山専用ボトルの中身の温度は、
T(t)-20 =118.7*e (-0.019594)*t-20
同じようにこの式をグラフ上にプロットすると、数のようになります。
うーん、まるでねつ造のようにきれいに一致していますね。(ねつ造ではありませんが…)
このグラフから、約20時間後までは60℃をキープしているであろうことがわかります。
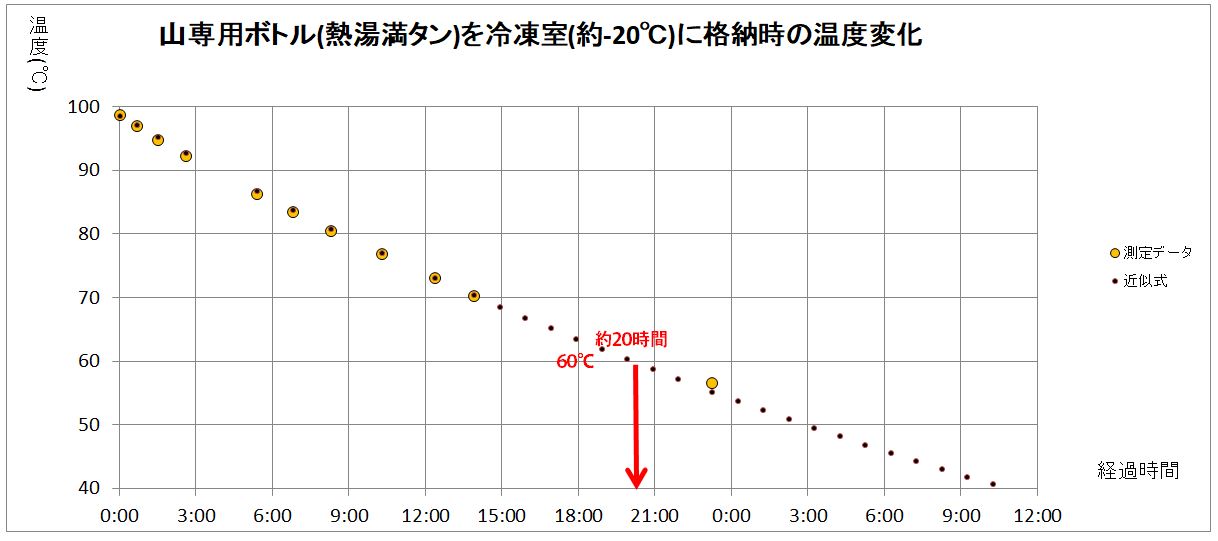
(3) 熱湯を半量入れて冷凍室(マイナス20℃)に格納した場合の温度変化
熱湯を山専用ボトルに入れた直後の温度が94.1℃なので、
時刻ゼロにおける外界(この場合は冷凍室)との温度差T0=94.1+20=114.1℃、
測定開始から11時間18分後(=11.3時間後)に、温度が59.6℃なので、このときの外界との温度差は 59.6+20=79.6℃
Λ=(LN(79.6/114.1))/(-11.3)=0.031864
よって、この場合の近似式は、
T(t)=114.1*e (-0.031864)*t
このときの山専用ボトルの中身の温度は、
T(t)-20 =114.1*e (-0.031864)*t-20
同じようにこの式をグラフ上にプロットすると、数のようになります。
データが乱れているように見えましたが、実際には1点がずれていただけでした。
このグラフから、約11時間後までは60℃をキープしていたであろうことがわかります。
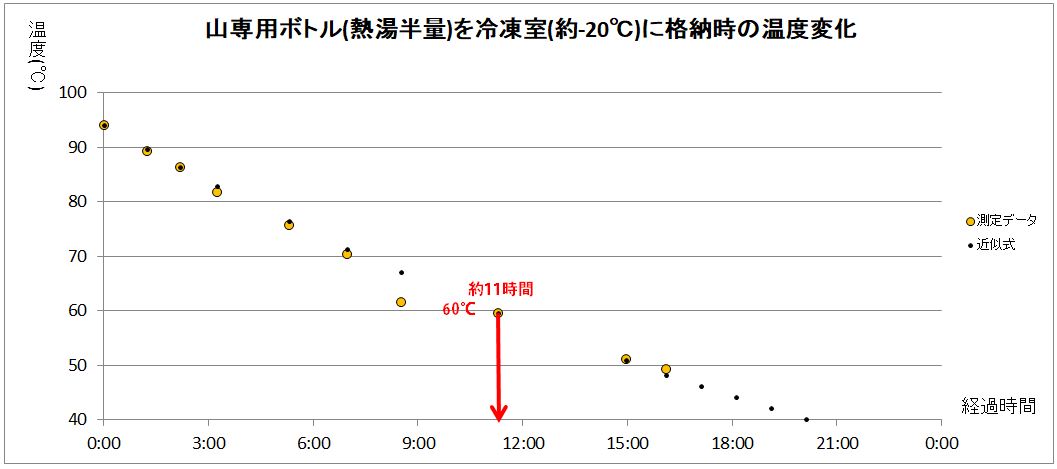
三つのグラフをまとめて描くと
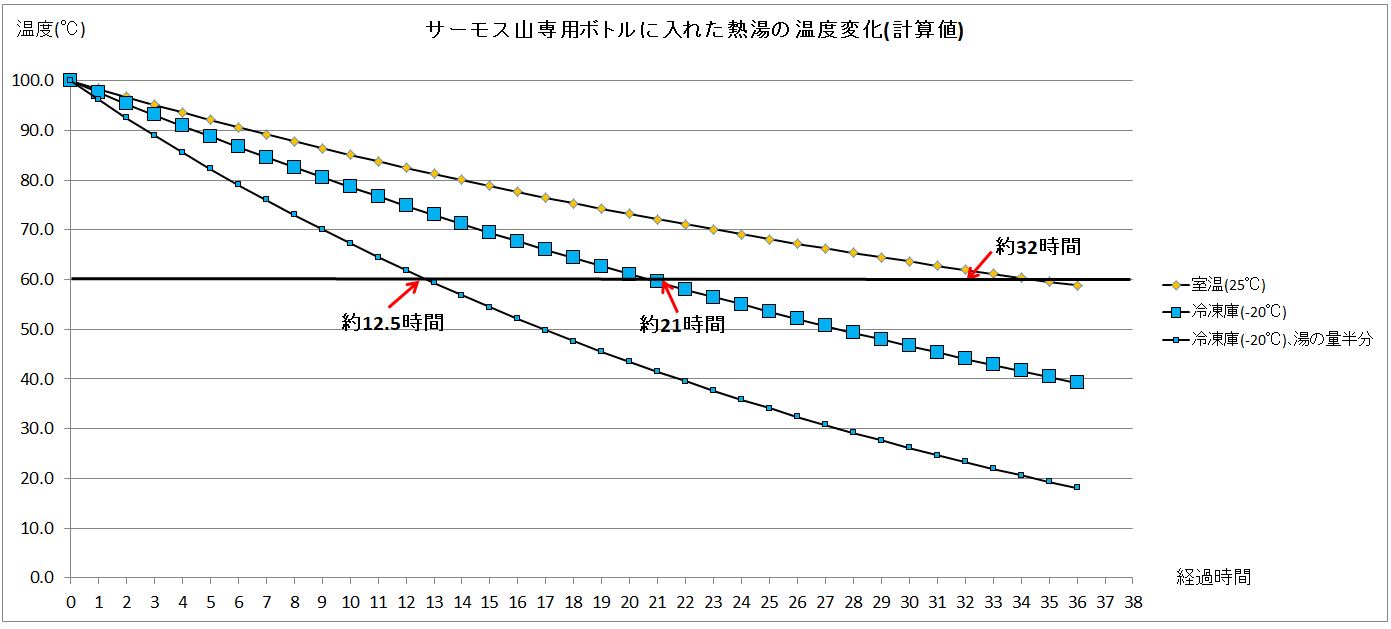
以上三つのグラフを一つにまとめてみると、下記のようになります。
なお、このグラフは最初の温度を100℃に変更してボトルの余熱を行った場合のグラフを近似しています。
まとめ
それぞれのグラフの式は、下記のようになります。
- 常温での冷却
T'(t)=(100-25)*e (-0.022118)*t+25
- マイナス20℃で、満タンの時の冷却
T'(t)=(100+20)*e (-0.019594)*t-20
- マイナス20℃で、半量の時の冷却
T'(t)=(100+20)*e (-0.031864)*t-20
ただし、(T(t)がボトルの中身と外気の温度差だったのに対して)T'(t)は、ボトルの中身の温度です。
また、tは経過時間(1時間=1)、eは自然対数の底(=2.71828…)です。
60℃がキープできる時間は、
- 常温での冷却
約32時間
- マイナス20℃で、満タンの時の冷却
約21時間
- マイナス20℃で、半量の時の冷却
約12.5時間
となります。
以上、読んでくださりありがとうございます。
この続きは、サーモス山専用ボトルの熱湯が何時間後に何℃になるか計算してみようをご覧下さい。
【寒さ対策】関連記事の一覧はこちらです。
