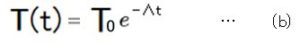Overview: Generate a equation which explains the relationship between the temperature of THERMOS bottle FFX-900 content, outside temperature, and elapsed time.
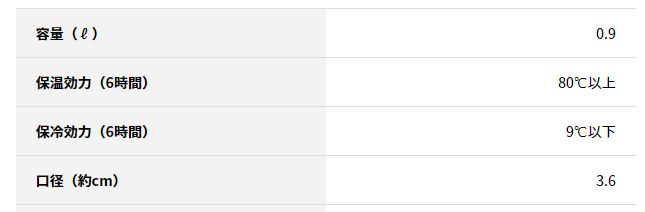
前回の記事 サーモス山専用ボトル FFX-900 に入れた熱湯が何時間後に何度に冷えているかを算出する公式を作ってみます。
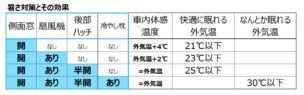
以前の記事 極寒に置かれたハイエースの温度がどのように変化するか を算出できる公式をご紹介したことがありました。
まず以前の記事と同様、指数関数的減衰
水筒の冷却を近似できる式は?
指数関数的減衰
指数関数的減衰は、下記の微分方程式で表されます。
これはつまり、
ある量( この場合はN) が減少するスピードは、N の大きさに比例する … ①
ということを表しています。
Q値
住宅の断熱度合い を表す数値として、熱損失係数 (Q 値) を用いますが、この値は、熱が逃げる速度 を表しています。この値が小さいほど、熱が逃げにくく、冬は暖かいことを表しています。
熱損失係数( Q 値)
そして、Q値 の単位は、W/m2 ・K (W=ワット、K=絶対温度)
つまり、Q値は単位面積、温度差 1 度あたり で熱が逃げる速度を表している定数 ですから、逆に考えると
ということです。
そして、もう一つ、一般的な事実として、
この二つを合わせると、
ものの温度は、外気との温度差に比例した速度で下がる … ②
ということになります。
これはつまり、熱いものはどんどん冷えますが、ある程度冷えてくると冷えるスピードもゆっくりになるということで、日常の経験に一致しています。
以上より
②のものの外気との温度差 は、①のN と同じ性質をもつので、指数関数的減衰の微分方程式を水筒の冷却状態を近似するのに使える (かもしれない)ことがわかります。
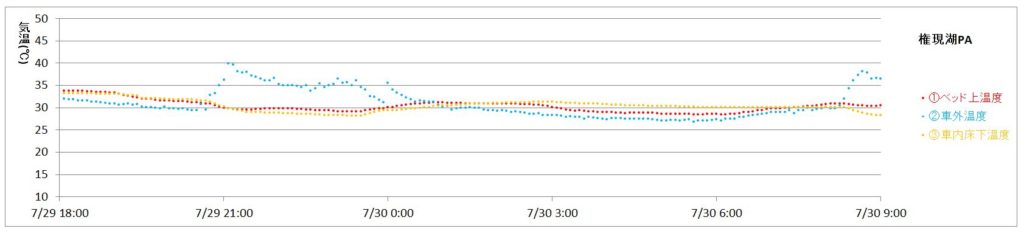
今回のグラフの近似式は?
ある時刻tにおける、ものの温度と外界の温度の差 T(t) は、T0 (時刻ゼロの時のT(t)の値)と、定数Λ (ラムダ)を用いて、下記のように表すことができます。(T0、 T(t) は、外界との温度差 であって、温度ではない ことに注意)
続きを読む